A continuación os dejo los últimos exámenes de la prueba de Selectividad de cada una de las comunidades autónomas de España.
En comunidades como Extremadura y Cantabria, además de los exámenes de las asignaturas de Física y Química, también están los de las restantes asignaturas de las que os podéis examinar en dichas comunidades.
PAU ANDALUCÍA
Examen Química Andalucía Junio 2010
Examen Química Andalucía Septiembre 2010
Examen Física Andalucía Junio 2010
Examen Física Andalucía Septiembre 2010
PAU ARAGÓN
Examen Química Aragón Septiembre 2009
Examen Física Aragón Septiembre 2009
PAU ASTURIAS
Examen Química Asturias Junio 2010
Examen Química Asturias Septiembre 2010
Examen Física Asturias Junio 2010
Examen Física Asturias Septiembre 2010
Examen Química Asturias Junio 2011
Examen Física Asturias Junio 2011
PAU CANTABRIA
Exámenes Cantabria Junio 2010
Exámenes Cantabria Septiembre 2010
PAU CASTILLA-LA MANCHA
Examen Castilla-La Mancha Física Junio2010
Examen Castilla-La Mancha Física Septiembre 2010
Examen Castilla- La Mancha Química Junio 2010
Examen Castilla-La Mancha Química Septiembre 2010
PAU CASTILLA Y LEÓN
Examen Castlla y León Física Junio 2011
Examen Castilla y León Química Junio 2011
PAU CATALUÑA
Examen Cataluña Física Junio 2011
Examen Cataluña Química Junio 2011
PAU EXTREMADURA
Exámenes Extremadura Junio 2010
Exámenes Extremadura Septiembre 2010
PAU GALICIA
Examen Galicia Física Junio 2010
Examen Galicia Química Junio 2010
PAU ISLAS BALEARES
Examen Islas Baleares Física Junio 2010
Examen Islas Baleares Química Junio 2010
PAU ISLAS CANARIAS
Examen Islas Canarias Física Junio 2010
Examen Islas Canarias Química Junio 2010
Examen Islas Canarias Física Junio 2011
Examen Islas Canarias Química Junio 2011
PAU LA RIOJA
Examen La Rioja Física Junio 2009
Examen La Rioja Química Junio 2009
PAU MADRID
Examen Madrid Física Junio 2010
Examen Madrid Química Junio 2010
PAU MURCIA
Examen Murcia Física Junio 2009
Examen Murcia Química Junio 2009
PAU NAVARRA
Examen Navarra Física Junio 2010
Examen Navarra Química Junio 2010
PAU PAÍS VASCO
Examen País Vasco Física Junio 2010
Examen País Vasco Química Junio 2010
PAU COMUNIDAD VALENCIANA
Examen Comunidad Valenciana Física Junio 2010
Examen Comunidad Valenciana Química Junio 2010
Fiquibach
viernes, 26 de agosto de 2011
martes, 28 de junio de 2011
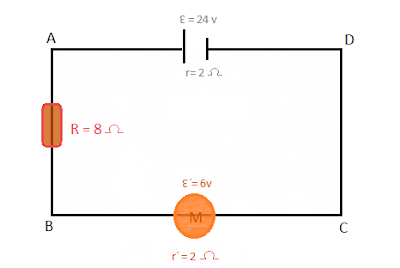
TEMA 12 : CIRCUITOS
Ejercicio:
Calcula:
a) La intensidad total que pasa por el circuito.
b) La potencia y la energía pasados 4 minutos.
c) La energía disipada en R.
d) La diferencia de potencial entre los puntos A y D y entre B y C.
e) La intensidad que pasaría por el circuito si el motor dejase de girar.
Solución :
a) I = 1,5 A b) P = 36 W ; E = 8640 J c) E = 4320 J d) VAD = 21 v ; VBC = 9 v e) I = 2A
Ejercicio:
Dado el siguiente circuito, calcula:
a) La intensidad total de corriente que pasa por el circuito.
b) La potencia consumida por el motor.
c) La intensidad que pasa por R2.
(Nota : Para facilitar la lectura de los datos sería conveniente que hiciérais click sobre la imagen del circuito).
Solución:
a) I = 0,16 A b) P = 1,36 w c) I = 0,048 A
Ejercicio:
Calcula la resistencia equivalente y la intensidad total que pasa por el circuito.
Solución :
Req = 99,8 Ω ; I = 0,12 A
Calcula:
a) La intensidad total que pasa por el circuito.
b) La potencia y la energía pasados 4 minutos.
c) La energía disipada en R.
d) La diferencia de potencial entre los puntos A y D y entre B y C.
e) La intensidad que pasaría por el circuito si el motor dejase de girar.
Solución :
a) I = 1,5 A b) P = 36 W ; E = 8640 J c) E = 4320 J d) VAD = 21 v ; VBC = 9 v e) I = 2A
Ejercicio:
Dado el siguiente circuito, calcula:
a) La intensidad total de corriente que pasa por el circuito.
b) La potencia consumida por el motor.
c) La intensidad que pasa por R2.
(Nota : Para facilitar la lectura de los datos sería conveniente que hiciérais click sobre la imagen del circuito).
 |
Solución:
a) I = 0,16 A b) P = 1,36 w c) I = 0,048 A
Ejercicio:
Calcula la resistencia equivalente y la intensidad total que pasa por el circuito.
Solución :
Req = 99,8 Ω ; I = 0,12 A
Ejercicio:
Calcula el calor disipado y la tensión a la que está sometida una resistencia fabricada con 4 m de hilo de aluminio cuya sección es de 0,2 mm2 si por ella pasa una intensidad de 108 mA durante 8 min.(Datos: Resistividad del Aluminio: 3,1 . 10 – 8 Ωm).
Solución :
E = 3,47 J ; V = 0,066 v.
TEMA 11 : ELECTROSTÁTICA
Ejercicio:
Calcula el campo eléctrico y el potencial en el punto C, sabiendo que las cargas situadas en el punto A y B valen cada una + 3 microculombios y que el triángulo equilátero tiene 4 m de lado. Calcula el trabajo necesario para llevar una carga positiva de 6 microculombios desde el infinito hasta el punto C.
Solución :
E = 2922,83 N/C ; V = 13500 v ; W = -0,081 J.
Ejercicio:
Se tienen dos cargas, una de 5 microculombios que está en el punto (4,0), y otra de - 3 microculombios situada en el punto (- 3,0). Calcula en qué punto se anulará el potencial creado por dichas cargas.
Solución :
P(- 0,375,0).
Ejercicio:
Se tienen 3 cargas q1 = 2 µC en el (2,0), q2 = - 4 µC en el (5,0) y q3 = 0,5 µC en el (7,0).Calcula el vector campo eléctrico producido por estas cargas en el punto A (6,0).
Solución :
E = - 39375 i
Ejercicio:
Tenemos dos hilos de longitud 40 cm que cuelgan desde el mismo punto y en cuyos extremos penden dos esferas de metal de masa 40 µg. Al quedar cargadas, dichas esferas se repelen hasta quedar separadas por una distancia de 4 cm. Calcula la carga de cada esfera.
Solución : q = 5,89 . 10-11 C
Calcula el campo eléctrico y el potencial en el punto C, sabiendo que las cargas situadas en el punto A y B valen cada una + 3 microculombios y que el triángulo equilátero tiene 4 m de lado. Calcula el trabajo necesario para llevar una carga positiva de 6 microculombios desde el infinito hasta el punto C.
Solución :
E = 2922,83 N/C ; V = 13500 v ; W = -0,081 J.
Ejercicio:
Se tienen dos cargas, una de 5 microculombios que está en el punto (4,0), y otra de - 3 microculombios situada en el punto (- 3,0). Calcula en qué punto se anulará el potencial creado por dichas cargas.
Solución :
P(- 0,375,0).
Ejercicio:
Se tienen 3 cargas q1 = 2 µC en el (2,0), q2 = - 4 µC en el (5,0) y q3 = 0,5 µC en el (7,0).Calcula el vector campo eléctrico producido por estas cargas en el punto A (6,0).
Solución :
E = - 39375 i
Ejercicio:
Tenemos dos hilos de longitud 40 cm que cuelgan desde el mismo punto y en cuyos extremos penden dos esferas de metal de masa 40 µg. Al quedar cargadas, dichas esferas se repelen hasta quedar separadas por una distancia de 4 cm. Calcula la carga de cada esfera.
Solución : q = 5,89 . 10-11 C
TEMA 10 : ENERGÍA
Ejercicio:
Se lanza un cuerpo de 2 kg verticalmente y hacia arriba a una velocidad de 20 m/ s. Calcula la altura máxima que alcanzará dicho cuerpo.
Solución :
h = 20,4 m
Ejercicio:
Calcula la velocidad inicial con la que se lanzó un cuerpo de 42 g hacia arriba, sabiendo que la altura máxima alcanzada fue 32 m.
Solución :
v = 25,04 m/s
Ejercicio:
Se lanza una bola de 5 Kg de masa por un plano inclinado hacia arriba con una velocidad inicial de 30 Km/ h. Sabiendo que el coeficiente de rozamiento es 0,2, calcula:
a) La velocidad que llevará cuando haya recorrido 2 m.
b) La altura máxima que alcanzará.
Solución :
a) v = 6,56 m/s ; b) h = 7,56 m
Ejercicio:
Se lanza en Marte verticalmente hacia arriba un cuerpo con una masa de 815 g a una velocidad de 20 m/s. Calcula, sabiendo que la gravedad en Marte vale 3,7 m/s²:
a) La altura máxima alcanzada y la energía potencial en ese punto.
b) La energía potencial y cinética a los 50 m del suelo marciano.
Solución:
a) hmáx = 54,05 m ; Ep = 163 N. b) Ep = 150,775 ; Ec = 12,225 N.
Ejercicio:
Se lanza un bloque de 2 Kg a una velocidad de 20 m/s hacia arriba por una rampa de pendiente 30º cuyo coeficiente de rozamiento se supone nulo.Calcula:
a) Cuánto vale la energía mecánica en la parte más alta y más baja de la rampa.
b) El espacio recorrido por el bloque antes de detenerse.
c) La energía potencial y cinética cuando ha recorrido 4 m.
Solución :
a) Em = Em' = 400 N. b) s = 40,8 m. c) Ep = 39,2 N ; Ec = 360,8 N.
Ejercicio:
Tenemos un objeto de 1 Kg sujeto a un muelle de constante K = 200 N/m sobre una mesa. El muelle se estira 10 cm y se suelta. Si entre el objeto y la mesa existe un rozamiento de coeficiente 0,2, ¿qué velocidad lleva el objeto cuando pasa por la posición x = 0 cm?
Solución :
v = 1,61 m/s
Ejercicio:
Sabiendo que la potencia de una bomba hidráulica es de 20 kW y que esta es capaz de expulsar 50 metros cúbicos en una hora. Calcula cuál es la altura máxima a la que puede mandar el agua.
Solución :
hmáx = 147,88 m.
Ejercicio:
Calcula el tiempo que tarda un calentador eléctrico de 3 kW para calentar 42 L de agua desde 23ºC hasta 42ºC.
Solución :
t = 18,53 min.
Ejercicio:
Se lanza una bola de 5 Kg de masa por un plano inclinado hacia arriba con una velocidad inicial de 30 Km/ h. Sabiendo que el coeficiente de rozamiento es 0,2, calcula:
a) La velocidad que llevará cuando haya recorrido 2 m.
b) La altura máxima que alcanzará.
Solución :
a) v = 6,56 m/s ; b) h = 7,56 m
Ejercicio:
Se lanza en Marte verticalmente hacia arriba un cuerpo con una masa de 815 g a una velocidad de 20 m/s. Calcula, sabiendo que la gravedad en Marte vale 3,7 m/s²:
a) La altura máxima alcanzada y la energía potencial en ese punto.
b) La energía potencial y cinética a los 50 m del suelo marciano.
Solución:
a) hmáx = 54,05 m ; Ep = 163 N. b) Ep = 150,775 ; Ec = 12,225 N.
Ejercicio:
Se lanza un bloque de 2 Kg a una velocidad de 20 m/s hacia arriba por una rampa de pendiente 30º cuyo coeficiente de rozamiento se supone nulo.Calcula:
a) Cuánto vale la energía mecánica en la parte más alta y más baja de la rampa.
b) El espacio recorrido por el bloque antes de detenerse.
c) La energía potencial y cinética cuando ha recorrido 4 m.
Solución :
a) Em = Em' = 400 N. b) s = 40,8 m. c) Ep = 39,2 N ; Ec = 360,8 N.
Ejercicio:
Tenemos un objeto de 1 Kg sujeto a un muelle de constante K = 200 N/m sobre una mesa. El muelle se estira 10 cm y se suelta. Si entre el objeto y la mesa existe un rozamiento de coeficiente 0,2, ¿qué velocidad lleva el objeto cuando pasa por la posición x = 0 cm?
Solución :
v = 1,61 m/s
Ejercicio:
Sabiendo que la potencia de una bomba hidráulica es de 20 kW y que esta es capaz de expulsar 50 metros cúbicos en una hora. Calcula cuál es la altura máxima a la que puede mandar el agua.
Solución :
hmáx = 147,88 m.
Ejercicio:
Calcula el tiempo que tarda un calentador eléctrico de 3 kW para calentar 42 L de agua desde 23ºC hasta 42ºC.
Solución :
t = 18,53 min.
lunes, 27 de junio de 2011
TEMA 9 : DINÁMICA
Ejercicio:
Nadal golpea con su raqueta una pelota de 125 g de masa que le llega con una velocidad de 12 m/s y la devuelve en la misma dirección y sentido contrario a 20 m/s. Si el tiempo de contacto entre la pelota y la raqueta fue de 0,01 s Calcula:
a) La fuerza que hace.
b) El impuso mecánico.
Solución:
a) F = 400 N; b) I = 4 N·s
Ejercicio:
Calcula la velocidad de retroceso de un cañón de 1 t (proyectil incluido) al disparar una granada de 10 kg con velocidad de 500 m/s.
Solución :
v = -5,05 m/s.
Ejercicio:
Un muelle fijado al techo tiene una longitud de 11,96 cm y 14,90 cm, cuando se cuelgan de él, respectivamente, unas masas de 20 y 50 kg. Calcula su constante elástica y su longitud sin deformación.
Ejercicio:
Un muelle se alarga 20 cm cuando ejercemos sobre él una fuerza de 24 N y su longitud es 40 cm al aplicar una fuerza de 1,5 N. Calcula:
a) El valor de la constante elástica del muelle.
b) La longitud inicial.
c) La longitud cuando se hace una fuerza de 4 N.
d) El alargamiento para una fuerza de 3 N.
Solución:
a) K = 5 N/m; b) lo =10 cm ; c) l = 90 cm ; d) l= 60 cm
Ejercicio:
Solución:
a) a = 4,9 m/s2 b) a = 1,9 m/s2
Ejercicio:
Dado el siguiente sistema calcula la aceleración con la que este se moverá, sabiendo que el coeficiente de rozamiento es 0,2.
Solución :
a = 5,12 m/s2
Nadal golpea con su raqueta una pelota de 125 g de masa que le llega con una velocidad de 12 m/s y la devuelve en la misma dirección y sentido contrario a 20 m/s. Si el tiempo de contacto entre la pelota y la raqueta fue de 0,01 s Calcula:
a) La fuerza que hace.
b) El impuso mecánico.
Solución:
a) F = 400 N; b) I = 4 N·s
Ejercicio:
Calcula la velocidad de retroceso de un cañón de 1 t (proyectil incluido) al disparar una granada de 10 kg con velocidad de 500 m/s.
Solución :
v = -5,05 m/s.
Ejercicio:
Un muelle fijado al techo tiene una longitud de 11,96 cm y 14,90 cm, cuando se cuelgan de él, respectivamente, unas masas de 20 y 50 kg. Calcula su constante elástica y su longitud sin deformación.
Solución:
K = 104 N/m; L = 0,1 m
Ejercicio:
Un muelle se alarga 20 cm cuando ejercemos sobre él una fuerza de 24 N y su longitud es 40 cm al aplicar una fuerza de 1,5 N. Calcula:
a) El valor de la constante elástica del muelle.
b) La longitud inicial.
c) La longitud cuando se hace una fuerza de 4 N.
d) El alargamiento para una fuerza de 3 N.
Solución:
a) K = 5 N/m; b) lo =10 cm ; c) l = 90 cm ; d) l= 60 cm
Ejercicio:
Un cuerpo desciende por un plano inclinado de 30º. Calcula la aceleración en los siguientes casos:
a) Si no hay rozamiento.
b) Si el coeficiente de rozamiento es 0,35.
Solución:
a) a = 4,9 m/s2 b) a = 1,9 m/s2
Ejercicio:
Dado el siguiente sistema calcula la aceleración con la que este se moverá, sabiendo que el coeficiente de rozamiento es 0,2.
Solución :
a = 5,12 m/s2
TEMA 8 : CINEMÁTICA
Ejercicio:
Ejercicio:
Desde la terraza de un piso situada a 10 m de altura se lanza verticalmente hacia arriba un objeto con velocidad de 30 m/s. Calcula:
Ejercicio:
Un avión que vuela horizontalmente a 1000 m de altura con una velocidad constante de 100 m/s , deja caer una bomba para que dé sobre un vehículo que está en el suelo. Calcula a qué distancia del vehículo, medida horizontalmente debe soltar la bomba.
Solución :
x = 1429 m
Ejercicio:
Si la rueda de un automóvil gira de manera constante a 1500 r.p.m. , un punto de la misma situado a
50 cm del eje de giro, ¿ qué movimiento lleva? ¿Tiene velocidad angular, lineal, aceleración y frecuencia? Si la respuesta es afirmativa calcula su valor.
Solución :
Movimiento circular uniforme; w = 157,08 rad/s; v = 78,04 m/s; f = 25 Hz.
Ejercicio:
En un semáforo hay un motorista de la policía parado. Un coche que lleva velocidad constante de 108 km/h
se salta dicho semáforo en rojo y en ese mismo instante arranca el policía con una aceleración de 0,75 m/s.
Calcula:
a) Cuánto tiempo tarda en alcanzar al coche.
b) Qué espacio recorre hasta alcanzarlo.
c) Velocidad de ambos en el momento del encuentro.
Solución: a) ∆t = 80 s; b) ∆x = 2400 m; c) vP = 60 m/s y vC = 30 m/s.
Ejercicio:
Desde la terraza de un piso situada a 10 m de altura se lanza verticalmente hacia arriba un objeto con velocidad de 30 m/s. Calcula:
a) Altura máxima.
b) Velocidad al llegar al suelo.
Solución: a) hmáx = 55,9 m; b) v = 33,02 m/s
Ejercicio:
Un avión que vuela horizontalmente a 1000 m de altura con una velocidad constante de 100 m/s , deja caer una bomba para que dé sobre un vehículo que está en el suelo. Calcula a qué distancia del vehículo, medida horizontalmente debe soltar la bomba.
Solución :
x = 1429 m
Ejercicio:
Si la rueda de un automóvil gira de manera constante a 1500 r.p.m. , un punto de la misma situado a
50 cm del eje de giro, ¿ qué movimiento lleva? ¿Tiene velocidad angular, lineal, aceleración y frecuencia? Si la respuesta es afirmativa calcula su valor.
Solución :
Movimiento circular uniforme; w = 157,08 rad/s; v = 78,04 m/s; f = 25 Hz.
Ejercicio:
Una lancha intenta atravesar un río con una velocidad constante de 25 m/s perpendicularmente a la corriente que lleva una velocidad de 15 m/s. Si la distancia total recorrida es 140 m. Calcula:
a) Anchura del río
b) Tiempo que tarda en cruzarlo.
c) Velocidad al llegar a la otra orilla.
Solución : a) x = 120 m; b) t = 4,8 s; c) v 29,15 m/s.
TEMA 7 : FORMULACIÓN ORGÁNICA
Formula los siguientes compuestos:
a) Propenonitrilo
b) Ácido 3-metil-2 pentenoico
c) Propanotriol
d) 3- etil- hexanodial
e)Etano
f) Etanamida
g) Nitrometano
h) Propanona
i) Tricloruro de metilo
j) 2- buteno
k) Etanol
l) Metano
m) Etilamina
n) 1- butino
ñ)Etilmetiléter
Solución:
a)

b)

c)
d)

e)

f)

g)

h)

i)

j)
k)

l)

m)

n)

ñ)

Ejercicio:
Nombra los siguientes compuestos:
a)

c)

d)

e)

f)
g)
h)
i)
j)
k)
l)
m)
n)

ñ)

Solución:
a) Triclorometano (Cloroformo)
b) Metanol
c) Metanal
d) Nitroetano
e) 3-buten-2-ona
f) 2-pentinodial
g) 1-etil-3-metil-benceno
h) 1,3-dimetil benceno
i) 1,2-dicloro, 1,2-pentanodiol
j) Ácido 3-amino-2-pentenodioico
k) 2-butenonitrilo
l) Propanoato de etilo
m) 2-pentinodial
n) N-etenil, N-etil,N-metil amina
ñ) Ácido etanoico
Suscribirse a:
Entradas (Atom)